Siirry pääsisältöön
Sisällysluettelo

Vanhentunut teksti: Matematiikka verkossa ja sähkökirjoissa

Julkaistu: 19.2.2023. Viimeksi päivitetty: 11.3.2024.

Kirjoittaja: Sami Määttä (sami.maatta@celia.fi), Saavutettavuuskirjasto Celia.

Huomio! Tämä artikkeli on vanhentunut! MathML tuki selaimissa on parantunut ja MathCAT-ruudunlukijalisäosaa suomennetaan. Sen avulla voi kuunnella ja lukea MathML-koodilla kirjoitettuja kaavoja pistenäytöltä.

Lue kirjoitukseni siitä, miten matematiikkaa kannattaa kirjoittaa tästä eteenpäin MathML-koodina.

Päivitysloki
  • 11.3.2024: Lisätty linkki uuteen kirjoitukseen matematiikan kirjoittamisesta saavutettavasti.
  • 22.2.2024: Artikkeli on vanhentunut, koska MathML tuki selaimissa on parantunut. Jatkossa on siis parempi kirjoittaa puhdasta MathML-koodia, sillä MathCAT-ohjelmisto voi tulkita sen oikeaksi ruudunlukijalle. Tästä tulee oma artikkeli myöhemmin.
  • 20.9.2023: Muokkasin suositukset-osiota selkeämmäksi. Paransin tekstin kieltä ja lisäsin linkin mukautetun AsciiMathin käyttöön.
  • 13.3.2023: Lisäsin kuhunkin kohtaan toimivan esimerkin.
  • 13.3.2023: Poistin kohdan, joka suositteli SVG-kuvan ja sen title-elementin käyttöä. Se ei toiminut tyydyttävästi ruudunlukijalla.

Kenelle dokumentti on?

Dokumentti on tarkoitettu kenelle tahansa, joka on kiinnostunut matematiikan saavutettavasta esittämisestä verkossa ja sähkökirjoissa.

Dokumentin ymmärtäminen ei edellytä verkkosivujen tai sähkökirjojen valmistamisen osaamista ennen kuin siinä esitellään koodiesimerkkejä. Käytännössä ratkaisut ovat HTML-pohjaisia.

Suositukset

Käytä MathML-koodia verkossa ja sähkökirjoissa. Sitä tuetaan monissa eri selaimissa ja standardia kehitetään aktiivisesti.

MathML-koodia ei kuitenkaan tueta suomen kielellä ohjelmissa tai apuvälineissä. Ole siis valmis paikkaamaan matematiikan esittämistä muilla keinoilla, jotta voit sanoa matematiikan merkintöjen olevan saavutettavia.

Tästä dokumentista löydät esimerkkejä matematiikan merkitsemiseen suomeksi ja pistekirjoituksella.

MathML-koodi ja sen tuki

MathML on XML-pohjainen merkintäkieli, jonka avulla voit esittää matemaattisia kaavoja ja symboleita verkkosivuilla sekä sähkökirjoissa. MathML on W3C:n (kansainvälinen web-standardeja ylläpitävä konsortio) suositus matemaattiseen merkintään verkossa: Katso Mathematical Markup Language (MathML) Version 3.0 2nd Edition (w3.org) (englanniksi).

Toimivia paikkaamisratkaisuja ovat LaTeX-koodi ja mukautettu AsciiMath, jonka lukemiseen pistekirjoitusta lukeva on tottunut. Tavoitteena on esittää matematiikka siten, että se on yhtä saavutettava henkilölle, joka ei käytä ruudunlukijaa ja sellaiselle, joka käyttää ruudunlukijaa.

Käyttämällä MathML-koodia kannustetaan näitä ohjelmistoja omaksumaan merkintä ja tekemään se toimivaksi. Mitä enemmän MathML-koodia käytetään, niin sitä useampi toimija alkaa sitä tukea.

Saavutettavuuskirjasto Celiaa vastaava kirjasto Norjassa (NLB) käyttää mallia. Huomaa, että inline ja block ovat toistensa vaihtoehtoja:

<math
  altimg="[kuvan sijainti]"
  alttext="[matematiikka tekstinä muulla tavalla (LaTeX tai Asciimath)]"
  display="[inline | block]"
  xmlns="<http://www.w3.org/1998/Math/MathML>"
>
  [MathML-koodi]
</math>

altimg-attribuutilla voi määrittää, että mikä kuva näkyy kaavan sijasta, jos MathML-koodia ei tueta.

alttext-attribuutilla voi määrittää, että mikä teksti näkyy MathML-koodin sijasta, jos sitä ei tueta. Tämä ei siis ole sama asia kuin kuvien alt-teksti.

MathML-tuki ruudunlukijoissa ja pistenäytöllä

Tiedosta, että MathML-koodille ei ole kattavaa tukea ruudunlukijoissa eikä pistenäytöissä suomen kielellä.

Huomaa, että jos jokin ratkaisu toimii ruudunlukijalla, niin siitä ei voi päätellä, että se toimisi myös pistenäytöllä saavutettavuusasiantuntija ja -auditoija Ronja Pahaojan mukaan Facebookissa (julkinen "Verkkopalvelujen saavutettavuus" -ryhmä).

MathML-koodin toimivuutta kannattaa siis testata eri apuvälineillä.

MathML-tuki selaimissa

Päivitys 2.3.2023: Lue ajantasainen listaus MathML-koodia tukevista selaimista taulukosta Mozillan Web Docsien MathML -osiosta (englanniksi).

Alla tiivistelmä suomeksi. Gecko-, Webkit- ja Chromium-pohjaiset selaimet tukevat MathML-koodia. Viimeisimpänä Chromium-pohjaiset vuoden 2023 alusta (chromestatus.com, englanniksi).

Siis MathML-koodi on tuettu ainakin selaimissa

Tähän mennessä MathML-koodin tuen puutetta on paikattu MathJax-lisäosalla (mathjax.org, englanniksi), jolla on edelleen käyttötarkoituksia, joten siihenkin kannattaa tutustua. Sen avulla voi esimerkiksi näyttää myös LaTeX-koodin lukijalle.

MathML-tuki EPUB3-sähkökirjaformaatissa

Käytä EPUB3-kirjaformaattia, kun teet sähkökirjoja. MathML-koodi on osa EPUB3-formaattia (W3C, englanniksi).

MathML-tuki lukuohjelmissa

On lukuohjelmia, jotka tukevat MathML-koodia EPUB-kirjoissa. Voit tarkistaa epubtest.org -sivuston taulukosta "Mathematics"-sarakkeen lajittelulla (englanniksi), millä käyttöjärjestelmillä ja ruudunlukijoilla tuki on. Huomaa, että tässä on testattu englanninkielisillä ohjelmilla.

Esimerkkejä lukuohjelmista

Matematiikan merkintöjen paikkaaminen

Koska MathML-tuki on vielä riittämätön suomeksi, tarjoa MathML-koodin ohella toisenlaisia tapoja lukea tai kuunnella matemaattinen sisältö. Älä kuitenkaan jätä MathML-koodia käyttämättä, koska niin kauan kuin sen käyttöä kierretään erilaisilla keinoilla, niin ohjelmistot eivät tule tukemaan sitä.

Mukautettu AsciiMath ja LaTeX

Pistekirjoituksen neuvottelukunta ylläpitää sivuja, joilta voi lukea matematiikan pistekirjoituksesta.

Pistekirjoitusta lukeva lukee matematiikkansa yleensä kahdella tavalla:

  1. pistekirjoituksena pistekirjoista, joissa pistemerkit ovat paperilta tunnusteltavia merkkejä
  2. pistekirjoitusnäytön avulla elektronisen kirjan mukautetuista AsciiMath -merkinnöistä.

Huomioita mukautetusta AsciiMath -merkinnästä:

Lue lisää mukautetun AsciiMathin käytöstä julkaisusta Matematiikan, fysiikan ja kemian merkinnät elektronisissa oppikirjoissa (pistekirjoitus.fi, sivulla on PDF-tiedosto).

LaTeX-koodia käytetään teknisten alojen ladontakielenä ja nykyään myös lukiossa matematiikan esittämiseen. Monet verkko-ohjelmistot myös ottavat LaTeX-koodia vastaan ja näyttävät sen oikein.

Vertailu pienen kreikkalaisen kirjaimen alfa suhteen:

Käytännössä korkeakouluissa pistekirjoitusta lukevat opiskelijat ovat saaneet luennoitsijan LaTeX-pohjat ja kurssikirjallisuutensa Celiasta mukautettuna AsciiMath -merkintänä tai välitettynä toisen maan erikoiskirjastosta. Tällä hetkellä opiskelija joutuu siis opettelemaan myös LaTeX-merkintätavat, jos tämä haluaa mielekkäästi opiskella matematiikkaa.

Huomautus: PDF-tiedostot, jotka ladotaan LaTeX-koodin pohjalta eivät ole saavutettavia. On kuitenkin olemassa paketteja, jotka pyrkivät tekemään näistäkin PDF-tiedostoista saavutettavia.

Esimerkkejä matematiikan esittämiseen

Mainitse sähkökirjassassi tai verkkosivuillasi, millä tavalla esität matematiikkasi. Sähkökirjoissa luonnollinen paikka on kirjan alkutiedoissa ja metatiedoissa. Verkkosivuilla luonnollinen paikka on saavutettavuusselosteessa.

Vaihtoehdoissa on koodiesimerkkejä mahdollisesti toimivista ratkaisuista. Näitä ei ole testattu kirjoittajan toimesta laajasti, vaan ne ovat koontia erilaisista ratkaisuista. Testaa toteutus käyttäjien kanssa. Jaa myös tietosi siitä, mikä toimii tai siitä, mikä ei toimi!

Koodiin on tehty myös omia merkintöjä hakasulkeiden [ ] sisälle. Vaihtoehdot ottavat huomioon, miten kaavan voisi toteuttaa suomeksi. Vaihtoehdot on esitetty suosittelujärjestyksessä.

Käytän toimivissa koodiesimerkeissä mukautettua AsciiMath-koodia.

1. Kaava MathML-koodina ja lisäksi vain ruudunlukijalle näkyvänä tekstinä

Osat, joista esimerkki koostuu

Siirry 1. koodiesimerkkien yli seuraavaan osioon.

Malli:

<math
  altimg="[kuvan sijainti]"
  alttext="[vaihtoehtoinen kaava LaTeXilla tai 
          mukautetulla AsciiMath-koodilla]"
  display="[inline | block]"
  xmlns="<http://www.w3.org/1998/Math/MathML>"
>
  [MathML-koodi]
</math>
<span class="sr-only">
  [vaihtoehtoinen kaava LaTeXilla tai mukautetulla AsciiMath-koodilla]
</span>
Koodiesimerkki 1 
<math
  altimg="images/math-001.png"
  alttext="x_0, x_1, x_2, ..., x_n, ..."
  display="inline"
  xmlns="<http://www.w3.org/1998/Math/MathML>"
>
  <mrow>
    <msub>
      <mi>x</mi>
      <mn>0</mn>
    </msub>
    <mo>,</mo>
    <msub>
      <mi>x</mi>
      <mn>1</mn>
    </msub>
    <mo>,</mo>
    <msub>
      <mi>x</mi>
      <mn>2</mn>
    </msub>
    <mo>,</mo>
    <mo>&#8230;</mo>
    <mo>,</mo>
    <msub>
      <mi>x</mi>
      <mi>n</mi>
    </msub>
    <mo>,</mo>
    <mo>&#8230;</mo>
  </mrow>
</math>
<span class="sr-only">x_0, x_1, x_2, ..., x_n, ...</span>

Toimiva koodiesimerkki 1:

x 0 , x 1 , x 2 , … , x n , … x_0, x_1, x_2, ..., x_n, ...

2. Kaava kuvana (SVG) ja vaihtoehtoinen kaava vain ruudunlukijalle näkyvänä tekstinä

Osat, joista esimerkki koostuu

Siirry 2. koodiesimerkkien yli seuraavaan osioon.

Malli:

<span aria-hidden="true">
  <svg
    xmlns:xlink="<http://www.w3.org/1999/xlink>"
    [dimensiot
    ja
    muut
    määrittelyt]
    role="img"
    focusable="false"
    xmlns="<http://www.w3.org/2000/svg>"
    aria-labelledby="[<title>:ssä käytetty tunniste]"
  >
    <title id="[tunniste]">[Kaava]</title>

    <defs aria-hidden="true">[Kuvan määrittely]</defs>

    <g [mahdolliset attribuutit] aria-hidden="true">[Kuvan määrittely]</g>
  </svg>
</span>
<span class="sr-only">
  [Kaava joko LaTeX- tai mukautetulla AsciiMath -merkinnällä]
</span>

Alla Ylioppilastutkintolautakunnan toteutus lyhyen matematiikan näkövammaisten kokeessa keväällä 2022. Kaava on esitetty mukautetulla AsciiMath -merkinnällä.

Koodiesimerkki 2. Varoitus: Paljon tekstiä. 
<span class="e-formula" aria-hidden="true">
  <svg
    xmlns:xlink="<http://www.w3.org/1999/xlink>"
    width="15.759ex"
    height="2.676ex"
    style="vertical-align: -0.782ex;"
    viewBox="0 -815.3 6784.9 1152.1"
    role="img"
    focusable="false"
    xmlns="<http://www.w3.org/2000/svg>"
    aria-labelledby="MathJax-SVG-1-Title"
  >
    <title id="MathJax-SVG-1-Title">(-9)\\cdot (42-35)</title>

    <defs aria-hidden="true">
      <path
        stroke-width="1"
        id="E1-LATINMODERNMAIN-28"
        d="M332 -238c0 -5 -5 -10 -10 -10c-2 0 -4 1 -6 2c-110 83 
          -215 283 -215 454v84c0 171 105 371 215 454c2 1 4 2 6 2c5 
          0 10 -5 10 -10c0 -3 -2 -6 -4 -8c-104 -78 -173 -278 -173 
          -438v-84c0 -160 69 -360 173 -438c2 -2 4 -5 4 -8Z"
      ></path>
      <path
        stroke-width="1"
        id="E1-LATINMODERNMAIN-2212"
        d="M722 250c0 -11 -9 -20 -20 -20h-626c-11 0 -20 9 -20 
            20s9 20 20 20h626c11 0 20 -9 20 -20Z"
      ></path>
      <path
        stroke-width="1"
        id="E1-LATINMODERNMAIN-39"
        d="M457 329c0 -215 -122 -351 -251 -351c-85 0 -139 41 -139 
          108c0 39 30 48 46 48c22 0 46 -15 46 -46c0 -17 -8 -46 -52 
          -46c27 -34 81 -36 98 -36c58 0 162 46 162 280v32c-23 -58 
          -64 -100 -125 -100c-112 0 -200 98 -200 223c0 75 23 117 64 
          162c43 45 92 63 147 63 c89 0 204 -68 204 -337zM365 421c0 
          46 -4 109 -16 141c-17 45 -50 79 -96 79c-35 0 -73 -13 -100 
          -63c-21 -37 -21 -84 -21 -138c0 -49 0 -99 18 -136c31 -63 
          77 -63 93 -63c88 0 122 97 122 180Z"
      ></path>
      <path
        stroke-width="1"
        id="E1-LATINMODERNMAIN-29"
        d="M288 208c0 -171 -105 -371 -215 -454c-2 -1 -4 -2 -6 
          -2c-5 0 -10 5 -10 10c0 3 2 6 4 8c104 78 173 278 173 
          438v84c0 160 -69 360 -173 438c-2 2 -4 5 -4 8c0 5 5 10 10 
          10c2 0 4 -1 6 -2c110 -83 215 -283 215 -454v-84Z"
      ></path>
      <path
        stroke-width="1"
        id="E1-LATINMODERNMAIN-22C5"
        d="M192 250c0 -29 -24 -53 -53 -53s-53 24 -53 53s24 53 53 
          53s53 -24 53 -53Z"
      ></path>
      <path
        stroke-width="1"
        id="E1-LATINMODERNMAIN-34"
        d="M471 165h-100v-87c0 -36 2 -47 76 -47h21v-31c-41 3 -94 
          3 -136 3s-94 0 -135 -3v31h21c74 0 76 11 76 
          47v87h-266v31l307 469c8 12 11 12 20 12c16 0 16 -6 16 
          -26v-455h100v-31zM300 196v373l-244 -373h244Z"
      ></path>
      <path
        stroke-width="1"
        id="E1-LATINMODERNMAIN-32"
        d="M449 174l-28 -174h-371c0 24 0 26 11 37l192 214c55 62 
          105 141 105 221c0 82 -43 163 -134 163c-58 0 -112 -37 -135 
          -102c3 1 5 1 13 1c35 0 53 -26 53 -52c0 -41 -35 -53 -52 
          -53c-3 0 -53 0 -53 56c0 89 74 181 187 181c122 0 212 -80 
          212 -194 c0 -100 -60 -154 -216 -292l-106 -103h180c22 0 88 
          0 95 8c10 15 17 59 22 89h25Z"
      ></path>
      <path
        stroke-width="1"
        id="E1-LATINMODERNMAIN-33"
        d="M457 171c0 -102 -91 -193 -213 -193c-109 0 -202 66 -202 
          157c0 44 32 58 56 58c29 0 56 -20 56 -56c0 -38 -31 -60 -66 
          -55c35 -59 110 -76 153 -76c44 0 113 29 113 165c0 98 -37 
          166 -119 166h-44c-17 0 -24 0 -24 11c0 10 7 11 15 12c7 0 
          31 2 39 3c25 1 59 4 89 52 c26 44 28 102 28 114c0 90 -55 
          112 -96 112c-36 0 -102 -13 -133 -62c15 0 62 0 62 -50c0 
          -29 -20 -51 -51 -51c-29 0 -51 19 -51 52c0 76 76 136 177 
          136c96 0 184 -56 184 -138c0 -79 -58 -149 -140 -176c104 
          -21 167 -99 167 -181Z"
      ></path>
      <path
        stroke-width="1"
        id="E1-LATINMODERNMAIN-35"
        d="M449 201c0 -127 -102 -223 -218 -223c-112 0 -181 
          -181 183c0 46 35 53 49 53c33 0 50 -25 50 -49s-17 -49 -50
          -49c-11 0 -14 1 -17 2c17 -59 74 -112 147 -112c46 0 83 26
          107 65c24 42 24 102 24 137c0 50 -2 89 -18 126c-8 18
          -33 64 -85 64 c-81 0 -118 -54 -129 -70c-4 -6 -6 -9 
          -13 -9c-14 0 -14 8 -14 26v296c0 16 0 24 10 24c0 0 4 0 
          12 -3c47 -21 93 -28 133 -28c67 0 116 20 136 29c5 3 8 
          3 8 3c7 0 10 -5 10 -11c0 -13 -70 -104 -193 -104c-32 0 
          -65 7 -85 13v-195c36 35 79 51 127 51 c108 0 190 -100 
          190 -219Z"
      ></path>
    </defs>

    <g
      stroke="currentColor"
      fill="currentColor"
      stroke-width="0"
      transform="matrix(1 0 0 -1 0 0)"
      aria-hidden="true"
    >
      <use xlink:href="#E1-LATINMODERNMAIN-28" x="0" y="0"></use>
      <use xlink:href="#E1-LATINMODERNMAIN-2212" x="389" y="0"></use>
      <use xlink:href="#E1-LATINMODERNMAIN-39" x="1168" y="0"></use>
      <use xlink:href="#E1-LATINMODERNMAIN-29" x="1668" y="0"></use>
      <use xlink:href="#E1-LATINMODERNMAIN-22C5" x="2280" y="0"></use>
      <use xlink:href="#E1-LATINMODERNMAIN-28" x="2780" y="0"></use>

      <g transform="translate(3170,0)">
        <use xlink:href="#E1-LATINMODERNMAIN-34"></use>
        <use xlink:href="#E1-LATINMODERNMAIN-32" x="500" y="0"></use>
      </g>

      <use xlink:href="#E1-LATINMODERNMAIN-2212" x="4393" y="0"></use>

      <g transform="translate(5394,0)">
        <use xlink:href="#E1-LATINMODERNMAIN-33"></use>
        <use xlink:href="#E1-LATINMODERNMAIN-35" x="500" y="0"></use>
      </g>

      <use xlink:href="#E1-LATINMODERNMAIN-29" x="6395" y="0"></use>
    </g>
  </svg>
</span>
<span class="sr-only">(-9) *(42 -35)</span>

Toimiva koodiesimerkki 2:

(-9) *(42 -35)

3. Kaava kuvana (PNG, GIF, JPG) ja vaihtoehtoisella tekstillä

Osat, joista esimerkki koostuu

Näytä matemaattinen kaava kuvana. Kuvan voi ottaa esimerkiksi MathML-koodin tuottamasta kaavasta.

Verrattuna SVG-kuviin, PNG- tai JPG-kuvat ’suttaantuvat’, kun niitä suurentaa näytöllä. Paremman puutteessa, käytä kaavan esittämisessä kuvana paremmuusjärjestystä

  1. PNG
  2. GIF
  3. JPG

Malli:

<img
  src="[kuvan sijainti]"
  alt="[kaava LaTeXilla tai mukautetulla AsciiMath-koodilla]"
/>

Esimerkki mukautettuna NLB:n mallista:

<img
  class="displaymath"
  src="images/math-001.png"
  alt="x_0, x_1, x_2, ..., x_n, ..."
/>

NLB:ssä tarjotaan myös “puhuttu” tekstiversio kaavasta, mutta toteutus on tämän dokumentin ulkopuolella.

Toimiva koodiesimerkki 3:

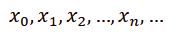
x_0, x_1, x_2, ..., x_n, ...

Kielen vaikutus matematiikan esittämiseen

Matematiikkaa kutsutaan “universaaliksi kieleksi”, mutta se ei pidä paikkansa pistekirjoituksella. Englanninkielisissä maissa käytetään matematiikassa UEB- (Unified English Braille) tai Nemeth-pistekirjoitusstandardia. Nykyään Nemethiä käytetään pitkälti Yhdysvalloissa ja UEB on edelleen käytössä Isossa-Britanniassa.

Jopa pohjoismaiden kesken käytetään erilaisia pistekirjoitusstandardeja. Suomessa näitä standardeja määrittää Pistekirjoituksen neuvottelukunta.

Pintapuolinen matematiikan pistekirjoitusvertailu Norjaan ja Ruotsiin

Norja

Norjassa peruslaskumerkinnät (Staped, norjaksi, sivulla on PDF-tiedosto) ovat samanlaiset kuin Suomessa. Eroja alkaa muodostua yksiköissä (prosentti, aste) ja muissa laskumerkinnöissä (suuruusvertailu, potenssi).

Ruotsi

Ruotsissa pistekirjoitusmerkinnät (MTM, ruotsiksi) ovat vain osittain tai epäsäännöllisesti samoja kuin Suomessa kuin Suomessa, mutta eroavat nopeasti. Esimerkiksi miinusmerkki on sama, mutta plus-merkki eri. Prosentin ja potenssin merkinnät ovat samat, mutta suuruusvertailun ja asteiden merkinnät erilaiset. MTM (”Myndigheten till tillgängliga medier” Ruotsissa) on tehnyt selvitystä matematiikan merkintätavoista (ruotsiksi, sivulla on PDF-tiedosto). Se ei kuitenkaan ota kantaa ratkaisuihin ja voi olla vanhentunut.

Pistekirjoitusmatematiikka suomeksi

Suomenkin sisällä pistekirjoitusmatematiikka jakautuu kahteen osaan: paperilta luettavaan ja koneelta luettavaan pistekirjoitusmatematiikkaan. Koneelta luettavat merkinnät ovat AsciiMath-koodiin pohjautuvia ja ne muistuttavat pistekirjoitusmatematiikkaa. AsciiMath-merkintää ei siis käytetä sellaisenaan, vaan se on mukautettua.

Haasteet matematiikan esittämiseen apuvälineille

Haasteeksi muodostuvat apuvälineiden tavat välittää tekstiä. AsciiMath-pohjaiset merkinnät toimivat pistenäytöllä, koska ne on tarkoitus lukea pistenäytöltä sellaisenaan. Ne ovat niin sanottua raakatekstiä (eng. "plain text") Kuuntelu ei ole mielekästä. AsciiMath-koodi ei ole täysin ymmärrettävää lukijalle, joka ei lue pistekirjoitusta.

Jos käytettäisiin pelkästään MathML-koodia, niin törmättäisiin kieliongelmaan: apuvälineet (ruudunlukijat ja pistenäytöt) eivät tue suomenkielistä standardia. On siis keksittävä muita vaihtoehtoja (kunnes joskus tulevaisuudessa suomenkielistä standardia tuettaisiin).

Tilanne nyt

Celian sähkökirjat

Celian sähkökirjoissa pistekirjoituksen lukijoille esitetään AsciiMath-pohjainen koodi, joka toimii pistenäytöllä, mutta ei juurikaan ruudunlukijan puhumana. Se ei sovi sellaisenaan matematiikan esittämiseen kaikille.

Korkeakoulut

Erityisesti tekniikan ja matematiikan aloilla matematiikkaa kirjoitetaan LaTeX-koodilla. Lopputuotteena on usein PDF-tiedosto, joka ei ole saavutettava. Luennoitsijoiden kannattaa vähintään antaa LaTeX-pohjansa pistekirjoitusta lukevalle opiskelijalle, koska se muistuttaa AsciiMath-koodia.

On keinoja lisätä LaTeX-koodilla tuotettujen PDF-tiedostojen saavutettavuutta (msu.edu, englanniksi). Työtä näiden suhteen jatketaan. Käsittääkseni tämä jää kuitenkin edelleen puolitiehen.

Haasteet matematiikan merkinnässä verkossa ja sähkökirjoissa

  1. Suomenkielistä ruudunlukijatukea ei ole matematiikan kaavoille MathML-koodilla.
  2. Matematiikan pistekirjoitusmerkinnät eroavat eri kielten välillä.
  3. Matematiikan pistekirjoitusmerkinnät muuttuvat siirryttäessä pistekirjoituksesta, elektroniseen pistekirjoitukseen (AsciiMath) ja edelleen jatko-opinnoissa LaTeX-koodin ymmärtämiseen.
  4. Lukuohjelmat tukevat vaihtelevasti MathML-käyttöä.
  5. MathML-pohjaisia matematiikan merkintöjen tuottamisen keinoja on ja näihin pitää tutustua. LaTeX-MathML -muunnosohjelmia tosin löytyy, mutta niiden käyttö voidaan kokea hankalaksi.
    • MathML-merkintöjen sijaan jatko-opintoja opiskelevat saavat todennäköisesti matematiikkansa LaTeX-koodina.

Muita haasteita matematiikan esittämisessä

Konteksti

Ei ole aina ilmeistä, että mitä halutaan esittää. Esimerkiksi halutaanko kaava x^2 ilmoittaa “luvun x neliö”, “x potenssiin kaksi” vai “x yläindeksi kaksi”. Tämä on kontekstisidonnaista ja "In the best of worlds, users will be able to decide how they want math communicated to them." Diagram Center, guidelines (englanniksi).

Lähteet

Lähteet ovat siinä järjestyksessä, jossa ne esiintyvä tekstissä.

  1. W3C:n MathML-spesifikaatio (englanniksi): https://www.w3.org/TR/MathML3/
  2. MathML-koodin attribuutteja (W3C, englanniksi), noudettu 2.3.2023: https://www.w3.org/TR/MathML/chapter2.html#interf.toplevel.atts
  3. Facebook-ryhmässä "Verkkopalvelujen saavutettavuus" Ronja Pahaojan kommentti ruudunlukijan ja pistenäytön yhteistoimivuudesta matematiikan merkinnöissä, noudettu 2.3.2023: https://www.facebook.com/groups/saavutettavuus/posts/3262911683835936/?comment_id=5403770139750069&reply_comment_id=5406069392853477&notif_id=1666777647499211&notif_t=group_comment_mention
  4. Taulukko selaimista, jotka tukevat MathML-koodia (Mozilla Web Docs), noudettu 2.3.2023: https://developer.mozilla.org/en-US/docs/Web/MathML#browser_compatibility
  5. Google Chrome -selaimen versio 109, joka tukee MathML-koodia (chromestatus.com, englanniksi): https://chromestatus.com/features#milestone%3D109
  6. Mathjax-lisäosan verkkosivut (englanniksi): https://www.mathjax.org/
  7. MathML on osa EPUB3-formaattia (W3C, englanniksi): https://www.w3.org/publishing/epub3/epub-contentdocs.html#sec-xhtml-mathml
  8. EPUB-kirjojen testaamista lukuohjelmissa. Järjestele "Mathematics"-sarakkeen mukaan (epubtest.org, englanniksi), noudettu 2.3.2023. https://epubtest.org/results
  9. Matematiikan, fysiikan ja kemian pistemerkinnät ja elektroniset merkinnät Suomessa (Pistekirjoituksen neuvottelukunta), noudettu 2.3.2023: https://www.pistekirjoitus.fi/julkaisut/matematiikka-ja-tietotekniikka/
  10. Lyhyen matematiikan ylioppilaskoe näkövammaisille (Yle Abitreenit), noudettu 2.3.2023: https://yle.fi/plus/abitreenit/2022/Kevät/2022-03-23_N_fi_vi/index.html
  11. StackOverflow'n esimerkki matematiikan merkitsemisestä (englanniksi), noudettu 2.3.2023: https://stackoverflow.com/questions/4697100/accessibility-recommended-alt-text-convention-for-svg-and-mathml
  12. Taustatietoa UEB-pistekirjoitusstandardista matematiikassa (Wikipedia, englanniksi).
  13. Norjan saavutettavia oppimateriaaleja valmistavan kirjaston dokumentti matematiikan opettamisesta (Statped, ruotsiksi), noudettu 2.3.2023: https://www.statped.no/laringsressurser/syn/matematikk-med-leselist-5.7.-trinn/
  14. Ruotsin saavutettavia kauno- ja tietokirjoja valmistavan kirjaston dokumentti matematiikan pistekirjoitusmerkinnöistä (MTM, ruotsiksi), noudettu 2.3.2023: https://www.mtm.se/punktskriftsnamnden/skrivregler-och-riktlinjer/matematik/
  15. Selvitys matematiikan merkintätavoista Ruotsissa MTM:n taholta (MTM; ruotsiksi), noudettu 2.3.2023: https://www.mtm.se/punktskriftsnamnden/skrivregler-och-riktlinjer/matematik/projekt-och-rapporter/
  16. Saavutettavien LaTeX-tiedostojen tekemisestä (Michiganin yliopisto, englanniksi), noudettu 2.3.2023: https://libguides.lib.msu.edu/c.php?g=995742&p=8207771
  17. Matematiikan kontekstisidonnaisuudesta kohdassa 4a. Math rendered in MathML (Diagram Center, englanniksi), noudettu 2.3.2023: http://diagramcenter.org/specific-guidelines-g.html

Muuta lisätietoa

Lista eurooppalaisista pistekirjoitusviranomaisista (euroblind.org, englanniksi, PDF), noudettu 2.3.2023: https://www.euroblind.org/sites/default/files/documents/ebu_list_of_braille_authorities_20220207.pdf