Lainasanat matematiikassamme

Julkaistu 30.8.2024. Aiheet: Suomeksi, Matematiikka, Kieli.

Aivan kuten suomen kielen asiantuntija saattaa välillä kavahtaa epämääräisiä lauserakenteita tai suoranaisia kirjoitusvirheitä, niin samoin käy matematiikan alan asiantuntijoille.

Viime aikoina silmiäni ovat rasittaneet (paremman sanan puutteessa) "lainasanat" tai anglismit eli englannin kielestä peräisin olevat suorat käännökset, jotka ovat suomeksi suoranaisia virheitä.

Matemaattisessa tekstissä näitä merkintöjä saatetaan katsoa enemmän läpi sormien kavahtamatta vakiintuneiden käytäntöjen vuoksi.

Prosenttiluvut

Englanninkielisessä tekstissä on tavallista kirjoittaa prosenttimerkki (%) yhteen luvun kanssa. Esimerkiksi "17%". Tämä on kuitenkin suomeksi väärin.

Oikea kirjoitusasu on jättää väli luvun ja prosenttimerkin välille "17 %".

Lisätietoa: Kielitoimiston ohjepankin artikkeli prosenttimerkistä.

Desimaalierotin

Toinen englanninkielisestä tekstistä tuttu tapa on kirjoittaa desimaaliluvut desimaalipisteen, eikä desimaalipilkun kanssa. Esimerkiksi "3.14".

Suomenkielinen kirjoitusasu on käyttää desimaalipilkkua "3,14".

Oletan, että desimaalipisteen käyttäminen on peruja monista ohjelmistoista, jotka käyttävät desimaalipistettä desimaalipilkun sijasta. Olisi työlästä vaihtaa esitystapaa esimerkiksi tieteellisissä julkaisuissa.

Lisätietoa: Kielikellon artikkeli pisteistä pilkuista.

Tuhaterotin

Englanninkielisessä tekstissä tuhaterottimena käytetään pilkkua, joka yhdistettynä desimaalipilkkuun voi tuottaa hämmentäviä hetkiä. Esimerkiksi "1,789" kirjoitetaan suomeksi "1 789".

Tässä täytyy huomioida, että käytetty väli on 'sitova välilyönti' (wikipedia), eikä suinkaan näppäimistöltä syntyvä välilyönnin tyhjä väli. Käytännössä tämä tarkoittaa sitä, että ruuduilla lukua ei jaeta välin kohdalta kahtia esimerkiksi rivinvaihdon takia.

Miljardit ja biljoonat

Miljardit ja biljoonat menevätkin iloisesti sekaisin aika ajoin eri paikoissa. Tämä johtuu siitä, että briteissä ja Yhdysvalloissa on käytetty niin sanottua 'lyhyttä asteikkoa' ja Suomessa (ja muuallakin maailmassa) käytetään 'pitkää asteikkoa'.

Miljoona (pitkä asteikko) on "million" (lyhyt asteikko) kummassakin asteikossa eli 10⁶. Erot alkavat heti tämän jälkeen:

Miljardi (pitkä asteikko) on "billion" (lyhyt asteikko) eli 10⁹.
Biljoona (pitkä asteikko) on "trillion" (lyhyt asteikko) eli 10¹².

Lisätietoa: Suurten lukujen nimet (wikipedia).

Norjan sijoitusrahasto

Erityisen hämmentäväksi tämä menee, kun nämä kaksi maailmaa kohtaavat. Innoitukseni tähän tekstiin tuli oikeastaan, kun näin Norjan rahastoja koskevan videon, jonka kommenteissa oltiin hämmentyineitä. Siellä ihmeteltiin, että oliko Norjalla nyt rahastossaan miljardeja kruunuja vai biljoonia dollareita - vai juuri toisinpäin.

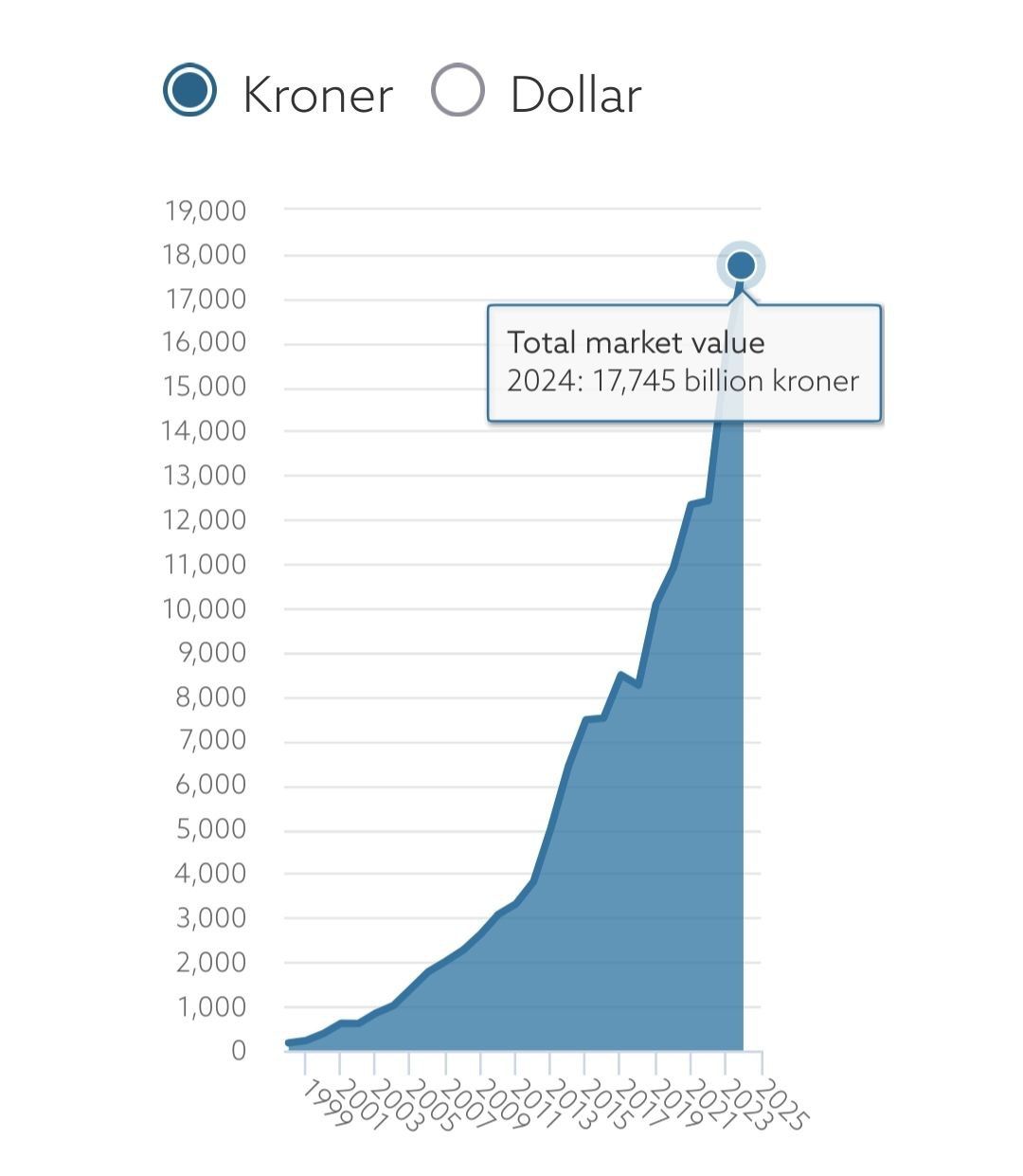
Kuvakaappaus viivakaaviosta, jossa rahaston arvo on noussut huimasti. Kaaviossa lukee, että vuonna 2024 sen arvo on 17,745 billion kroner.

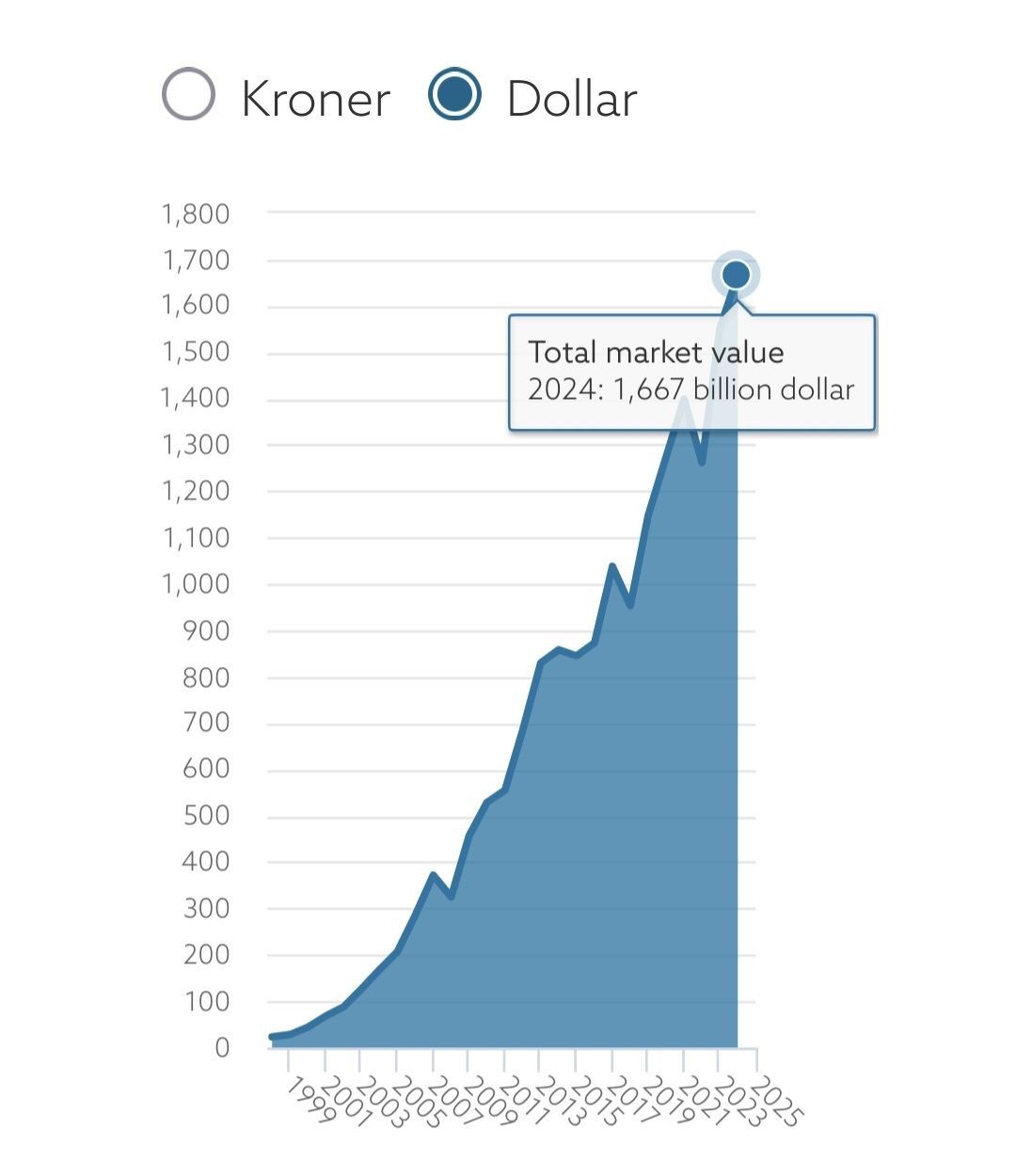
Sama kaavio kuin edellä, mutta dollareissa. Kaaviossa lukee, että vuonna 2024 sen arvo on 1,667 billion dollar.

Kuvien lähde: Norges Bank Investment Management (nbim.no)

No, niin. Kaavioissa on parikin haastavaa asiaa.

Englanninkielisyys kummassakin kaaviossa.
Valuuttamuunnos kruunuista dollareihin.

Käännettynä suomeksi rahaston arvo on siis

Norjan kruunuissa 17 745 miljardia
dollareissa 1 667 miljardia.

Luvut ja numerot

Suomeksi luku koostuu yksittäisistä numeroista. Englanninkielisessä tekstissä luku on "number" ja numero on "digit".

On siis sinänsä ymmärrettävää, että nämä sanat menevät sekaisin.

Yksiköt

Luulen, että seuraava on vain yleinen kirjoitusvirhe, eikä niinkään lainattu mistään. Yksikön kirjoittaminen ilman väliä lukuun. Esimerkiksi "6km", kun pitäisi kirjoittaa "6 km".

Yhteenkirjoitettua kirjoitusasua ei ole siis käytössä edes englanninkielisessä tekstissä.

Poikkeuksena tähän ovat (ainakin) prosenttiluvut ja valuutat. Englanninkielisessä tekstissä kirjoitettaisiin "15£" tai "42$". Suomeksi kirjoitetaan "16 €" tai "54 $".

Lisätietoa: Kielikellon artikkeli valuuttojen kirjoittamisesta.

Ainutlaatuisuuksia suomen kielessä

Nämä eivät ole varsinaisesti enää tyypillistä kielioppia, vaan enemmänkin kyse on siitä, miten matematiikassakin käytetyt merkinnät eivät ole yhteisiä kaikilla kielillä.

Laventaminen ja supistaminen

Murtolukujen laventamista ja supistamista ei ole samalla tavalla englannin kielessä, eikä sille ole siellä omaa merkintääkään.

Laventaminen: $_{}^{3)} \frac{2}{3} .$

Supistaminen: ${\frac{10}{15}}^{(5} .$

Loppujen lopuksi näiden merkintöjen käyttö on vain apuväline oman ajattelun näyttämisessä. Kun periaatteen ymmärtää, niin niitä ei erikseen tarvitse merkitäkään.

Integraalimerkintä

Suomessa käytetään integraalilaskennassa myös eräänlaista välimerkintää, joka on verrattavissa laventamisen ja supistamisen merkitsemiseen. Sitäkään ei varsinaisesti tarvitse tehdä, mutta opetteluvaiheessa se on hyödyllinen.

Ennen sijoittamista funktio integroidaan, jotta sijoittaminen ja laskeminen olisi helpompaa: 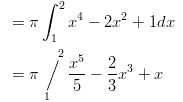Kuvakaappus kaksirivisestä integraalilaskusta. Toisessa vaiheessa integraalimerkki on korvattu suurella kenoviivalla, jolla on ala- ja yläraja.

Sille on myös vastine englanninkielisessä tekstissä:

= π (\frac{x^{5}}{5} - \frac{2}{3} x^{3} + x) |_{x = 1}^{x = 2} .

Bonus: Matematiikan pistekirjoitus

Suomessa on oma standardi matematiikan pistekirjoitukselle. Niin on myös Ruotsissa ja Norjassa, mutta nämä eivät ole keskenään samanlaisia. Matematiikka ei siis ole pistekirjoituksena yhteistä kaikille kielille.

Sen sijaan pistenuottikirjoitus on.