Käytännön matematiikkaa: Betonin paksuus

Julkaistu 18.6.2024. Aiheet: Suomeksi, Matematiikka, Käytännön matematiikkaa.

Kaverini työskentelee alalla, jolla oli olennaista tietää betonin paksuus tietyssä kohtaa. Betoni oli valettu kulmassa, jolloin suoraan ylhäältä otettu paksuus $x$ ei riittänyt, vaan myös pinnan kanssa kohtisuora paksuus $y$ haluttiin tietää myös.

Valokuva piirroksesta. Suunnikas, jonka alareunassa on kaltevuus, vasen sivu on x ja kohtisuora paksuus y. Vasen yläkulma on alfa. — Lähtötilanne, jossa betoni on valettu 28 prosentin kaltevuuskulmaan.

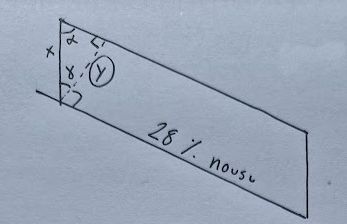
Mitä siis tiedetään? Mitattu paksuus $x$ ja 28 prosentin nousu.

Huomasin, että suunnikkaan kulmaan muodostuu suorakulmainen kolmio, jonka kulmat ovat $α$ ja $γ$ . Jäljelle jäänyt kulma on luonnollisesti suora kulma eli 90 asteen kulma.

Kaltevuuskulman prosentit voi ajatella niin, että jos edetään 100 metriä, niin pinta nousee samalla matkalla 28 metriä. Koska kyseessä on suunnikas, niin tiedetään, että sen vastakkaiset sivut ovat keskenään yhdensuuntaiset. Tällöin janoja jatkamalla voidaan tutkia samankohtaisia kulmia.

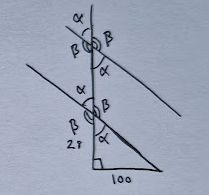
Valokuva piirroksesta. Selitetty yllä olevassa tekstissä. — 100 metrin eteneminen ja 28 metrin nousu. Kulmien $α$ ja $β$ samankohtaisuus.

Tästä saadaan kätevästi selvitettyä kulman $α$ suuruus, koska se muodostuu suorakulmaisen kolmion sisään, jonka sivujen pituudet tiedetään. Trigonometriasta tunnetaan, että tangentti (merkitään $tan$ ) tarkoittaa $\frac{vastainen kateetti}{viereinen kateetti}$ .

Kulman $α$ vastaisen kateetin pituus on 100 ja viereisen kateetin 28.

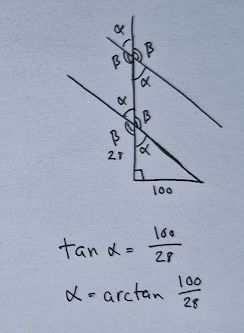
Valokuva piirroksesta. Suunnikkaaseen muodostuu alfan ja betan kanssa samankohtaisia ja täten samansuuruisia kulmia. Alla tangetin avulla muodostettu yhtälö. — Lasketaan kulman $α$ suuruus trigonometrian avulla.

Trigonometrian avulla saadaan aikaan alla oleva yhtälö ja se ratkaistaan:

\begin{matrix} tan α & = & \frac{100}{28} \\ ⇔ & α & = & arctan \frac{100}{28} . \end{matrix}

Valokuva piirroksesta. Suunnikkaan vasempaan kulmaan muodostuvassa suorakulmaisessa kolmiossa kulmaa alfa vastapäätä on sivu y ja vieressä sivu x. — Yhdistettynä alkuperäiseen tilanteeseen saadaan ratkaistava yhtälö.

Tilanteesta muodostetaan nyt yhtälö ja ratkaistaan se:

\begin{matrix} sin α & = & \frac{y}{x} \\ ⇔ & y & = & x \cdot sin α . \end{matrix}

Yhdistetään tähän tietoon ylempi yhtälö, josta saimme kulman $α$ lausekkeen

y = x \cdot sin (arctan \frac{100}{28}) = x 0.962... \approx 0.96 x .

Nähdään siis, että kohtisuora paksuus $y$ on jopa 96 prosenttia suoraan ylhäältä mitatusta paksuudesta $x$ . Jos sanottaisiin, että suoraan ylhäältä mitattu paksuus olisi 1 metri, niin kohtisuora paksuus olisi 0,96 metriä. Siis jos käyttäisi vain arvoa $x$ , niin heittoa syntyisi 4 senttimetriä.

Kaiken kaikkiaan kiva

Kun on opiskellut pitkän aikaa matematiikkaa, joka on monessa suhteessa teoreettista, niin käytännön esimerkit siitä, mitä on oppinut ovat todella kivoja. Aineenopettajanakin aika kuluu pitkälti kuviteltujen tilanteiden hahmotteluun, joista ei saa samanlaista nautintoa kuin siitä, että on todella ratkaissut jotain, mistä on konkreettista hyötyä.